최대 공약수
두 수의 최대 공약수는 두 수가 서로 공통으로 가지고 있는 약수 중 가장 큰 수
최대 공약수 예시
12의 약수 [1,2,3,4,6,12]
18의 약수 [1,2,3,6,9,18]
12와 18의 공약수는 [1,2,3,6]
12와 18의 최대공약수는 [6]
최대 공약수 구하는 방법
숫자가 2개인경우
1.두수를 공약수로 계속 나눈다.
2.공약수로 나눈 몫이 서로소가 되면 끝.
3.공약수를 모두 곱한다.
| 공약수 | 값1 | 값2 |
| 2 | 60 | 48 |
| 2 | 30 | 24 |
| 3 | 15 | 12 |
| 5 | 4 |
60과 48의 최대 공약수는 12
숫자가 3개인 경우(코드에서 배열을 매개변수로 주는 경우)
1.모든 수를 동시에 나눌수 있는 수로 나누다.
2.더이상 나누어질 수 없으면 끝.
3.공약수를 모두 곱한다.
| 공약수 | 값1 | 값2 | 값3 |
| 2 | 60 | 48 | 40 |
| 2 | 30 | 24 | 20 |
| 15 | 12 | 10 |
60과 48과 40의 최대공약수는 4
최소공배수
두 수의 최소공배수는 두 수에 서로 공통으로 존재하는 배수 중 가장 작은 수
최소공배수 예시
8의 배수 [8,16,24,32….]
10의 배수 [10,20,30,40….]
8과 10의 공배수 [40,80….]
8과 10의 최소공배수 [40]
최소 공배수 구하는 방법
숫자가 2개인 경우
1.두 수의 공약수로 나눈 몫이 서로소가 될 때까지 나누다.
2.공약수들과 서로스를 모두 곱한다.
| 공약수 | 값1 | 값2 |
| 2 | 60 | 48 |
| 2 | 30 | 24 |
| 3 | 15 | 12 |
| 5 | 4 |
60과 48의 최소공배수는 240
숫자가 3개이상인 경우(코드에서 배열을 매개변수로 주는 경우)
1.서로소가 아닌 수가 2개라도 있으면 그 수들의 공약수로 나눈다. 나누어 떨어지지 않는 수는 그대로 밑으로 내려온다.
2.모든 몫이 서로소이면 끝.
3.공약수와 아래 서로소를 모두 곱한다.
| 공약수 | 값1 | 값2 | 값3 |
| 2 | 60 | 48 | 40 |
| 2 | 30 | 24 | 20 |
| 2 | 15 | 12 | 10 |
| 5 | 15 | 6 | 5 |
| 3 | 3 | 6 | 1 |
| 1 | 2 | 1 |
60과 48과 40의 최소 공배수는 240
유클리드 호제법
2개 수의 최대 공약수를 구하는 알고리즘이다.
자연수 a,b에 대해서 a를 b로 나눈 나머지를 r 이라 한다면,
a%b = r
a,b의 최대 공약수s1와 b, r의 최대 공약수s2와 같다
a,b->s1 = b,r -> s2 -> s1=s2
이 성질에 따라 a를 b로 나눈 나머지 r1을 구하고 b를 r1로 나눈 나머지r2을 구한다
나머지 0이 될 때 나눈 수가 a,b의 최대 공약수가 된다.
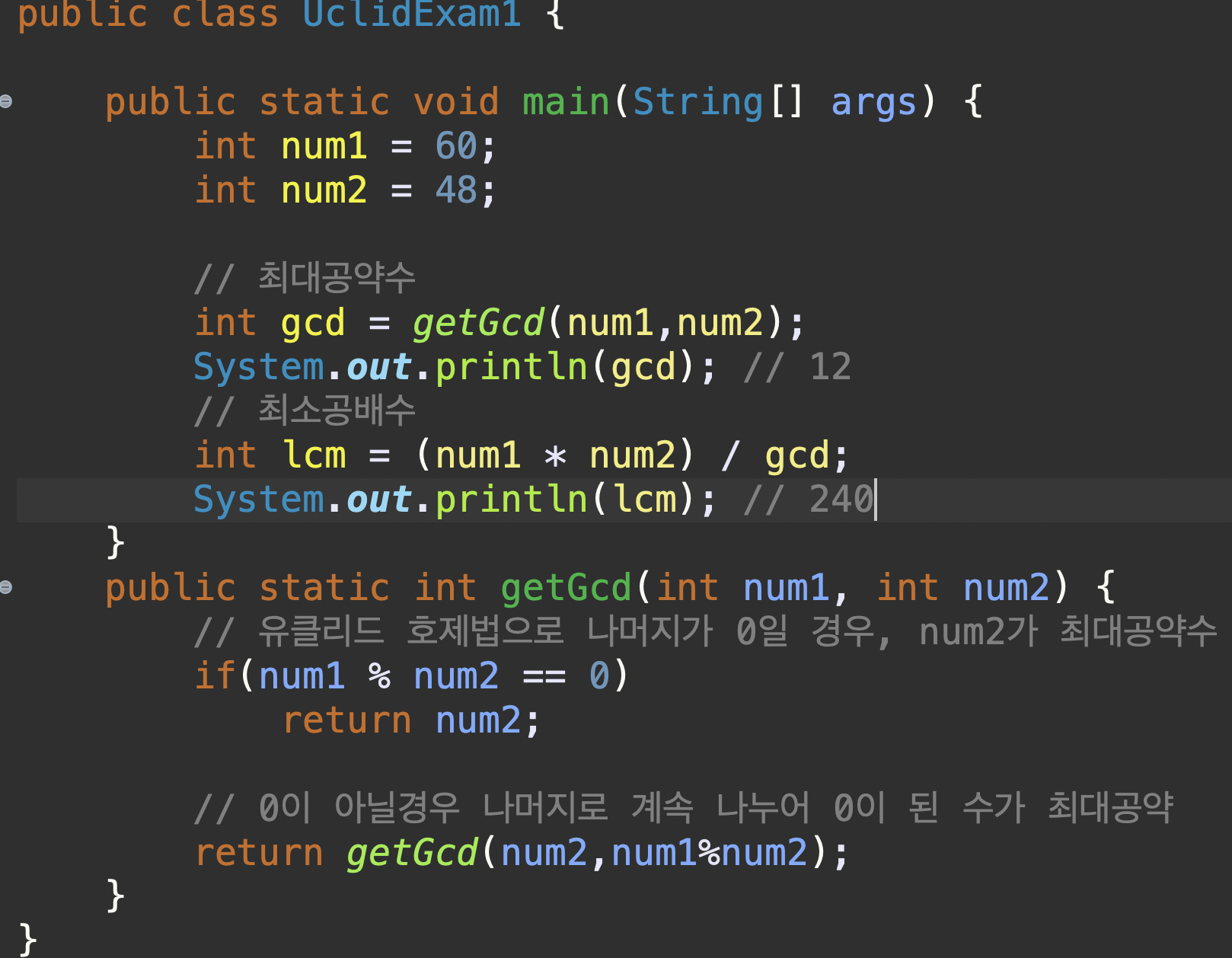
유클리드 호제법 예시
유클리드 호제법 최대공약수
60과 48의 최대 공약수
60 % 48 = 12
48 % 12 = 0 그러므로 최대공약수는 12이다.
유클리드 호제법 최소공배수
유클리드 호제법으로 최대공약수를 구한다음, 최소 공배수는 다음 식에 의해 구해진다.
최소 공배수 (a*b)/최대공약수
위의 예시를 따라
60 * 48 / 12 = 240 그러므로 최소공배수는 240이다.
만약 수가 여러개(배열)로 주어진다면 최소 공배수와 공약수를 어떻게 구하면 될까?
1.a,b의 최소 공배수를 구한다.
2.1에서 구한 a,b,의 최소공배수와 c의 최소공배수를 구한다.
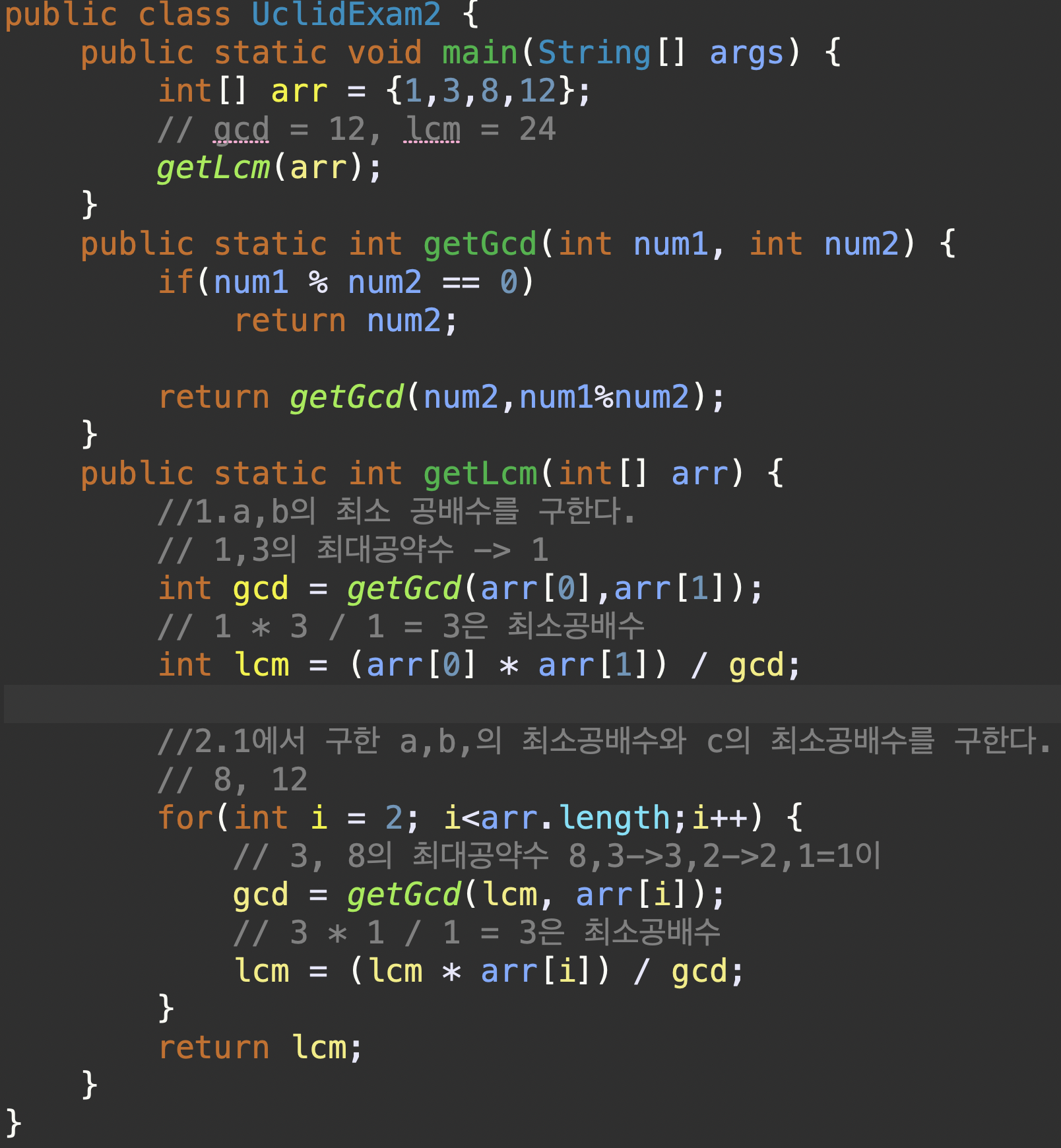
참고
https://programmer-chocho.tistory.com/9
[JAVA] 최대 공약수(GCD), 최소 공배수(LCM) 구하기
최대 공약수 구하는 방법 1. 숫자가 2개인 경우 1) 두 수를 공약수로 계속 나눈다. 2) 공약수로 나눈 몫이 서로소가 되면 stop 3) 왼쪽 공약수를 모두 곱한다. ∴ 60 과 48의 최대 공약수 : 2 ✕ 2 ✕ 3 = 1
programmer-chocho.tistory.com
'코테 > 개념 정리' 카테고리의 다른 글
| 제곱근과 합성수 간의 관계 (1) | 2023.12.01 |
|---|---|
| [Java]. 정수 오버플로우(overflow) (0) | 2023.11.30 |
| [Java]. BigInteger클래스 - 매우 큰 정수 표현 (0) | 2023.11.30 |
| 경우의 수 - 조합(n개의 원소중에서 r개를 선택하여 나열) (0) | 2023.11.30 |
| 경우의 수 - 순열(n개의 원소에서 r개를 선택하여 나열) (0) | 2023.11.30 |
최대 공약수
두 수의 최대 공약수는 두 수가 서로 공통으로 가지고 있는 약수 중 가장 큰 수
최대 공약수 예시
12의 약수 [1,2,3,4,6,12]
18의 약수 [1,2,3,6,9,18]
12와 18의 공약수는 [1,2,3,6]
12와 18의 최대공약수는 [6]
최대 공약수 구하는 방법
숫자가 2개인경우
1.두수를 공약수로 계속 나눈다.
2.공약수로 나눈 몫이 서로소가 되면 끝.
3.공약수를 모두 곱한다.
| 공약수 | 값1 | 값2 |
| 2 | 60 | 48 |
| 2 | 30 | 24 |
| 3 | 15 | 12 |
| 5 | 4 |
60과 48의 최대 공약수는 12
숫자가 3개인 경우(코드에서 배열을 매개변수로 주는 경우)
1.모든 수를 동시에 나눌수 있는 수로 나누다.
2.더이상 나누어질 수 없으면 끝.
3.공약수를 모두 곱한다.
| 공약수 | 값1 | 값2 | 값3 |
| 2 | 60 | 48 | 40 |
| 2 | 30 | 24 | 20 |
| 15 | 12 | 10 |
60과 48과 40의 최대공약수는 4
최소공배수
두 수의 최소공배수는 두 수에 서로 공통으로 존재하는 배수 중 가장 작은 수
최소공배수 예시
8의 배수 [8,16,24,32….]
10의 배수 [10,20,30,40….]
8과 10의 공배수 [40,80….]
8과 10의 최소공배수 [40]
최소 공배수 구하는 방법
숫자가 2개인 경우
1.두 수의 공약수로 나눈 몫이 서로소가 될 때까지 나누다.
2.공약수들과 서로스를 모두 곱한다.
| 공약수 | 값1 | 값2 |
| 2 | 60 | 48 |
| 2 | 30 | 24 |
| 3 | 15 | 12 |
| 5 | 4 |
60과 48의 최소공배수는 240
숫자가 3개이상인 경우(코드에서 배열을 매개변수로 주는 경우)
1.서로소가 아닌 수가 2개라도 있으면 그 수들의 공약수로 나눈다. 나누어 떨어지지 않는 수는 그대로 밑으로 내려온다.
2.모든 몫이 서로소이면 끝.
3.공약수와 아래 서로소를 모두 곱한다.
| 공약수 | 값1 | 값2 | 값3 |
| 2 | 60 | 48 | 40 |
| 2 | 30 | 24 | 20 |
| 2 | 15 | 12 | 10 |
| 5 | 15 | 6 | 5 |
| 3 | 3 | 6 | 1 |
| 1 | 2 | 1 |
60과 48과 40의 최소 공배수는 240
유클리드 호제법
2개 수의 최대 공약수를 구하는 알고리즘이다.
자연수 a,b에 대해서 a를 b로 나눈 나머지를 r 이라 한다면,
a%b = r
a,b의 최대 공약수s1와 b, r의 최대 공약수s2와 같다
a,b->s1 = b,r -> s2 -> s1=s2
이 성질에 따라 a를 b로 나눈 나머지 r1을 구하고 b를 r1로 나눈 나머지r2을 구한다
나머지 0이 될 때 나눈 수가 a,b의 최대 공약수가 된다.
유클리드 호제법 예시
유클리드 호제법 최대공약수
60과 48의 최대 공약수
60 % 48 = 12
48 % 12 = 0 그러므로 최대공약수는 12이다.
유클리드 호제법 최소공배수
유클리드 호제법으로 최대공약수를 구한다음, 최소 공배수는 다음 식에 의해 구해진다.
최소 공배수 (a*b)/최대공약수
위의 예시를 따라
60 * 48 / 12 = 240 그러므로 최소공배수는 240이다.

만약 수가 여러개(배열)로 주어진다면 최소 공배수와 공약수를 어떻게 구하면 될까?
1.a,b의 최소 공배수를 구한다.
2.1에서 구한 a,b,의 최소공배수와 c의 최소공배수를 구한다.

참고
https://programmer-chocho.tistory.com/9
[JAVA] 최대 공약수(GCD), 최소 공배수(LCM) 구하기
최대 공약수 구하는 방법 1. 숫자가 2개인 경우 1) 두 수를 공약수로 계속 나눈다. 2) 공약수로 나눈 몫이 서로소가 되면 stop 3) 왼쪽 공약수를 모두 곱한다. ∴ 60 과 48의 최대 공약수 : 2 ✕ 2 ✕ 3 = 1
programmer-chocho.tistory.com
'코테 > 개념 정리' 카테고리의 다른 글
| 제곱근과 합성수 간의 관계 (1) | 2023.12.01 |
|---|---|
| [Java]. 정수 오버플로우(overflow) (0) | 2023.11.30 |
| [Java]. BigInteger클래스 - 매우 큰 정수 표현 (0) | 2023.11.30 |
| 경우의 수 - 조합(n개의 원소중에서 r개를 선택하여 나열) (0) | 2023.11.30 |
| 경우의 수 - 순열(n개의 원소에서 r개를 선택하여 나열) (0) | 2023.11.30 |
