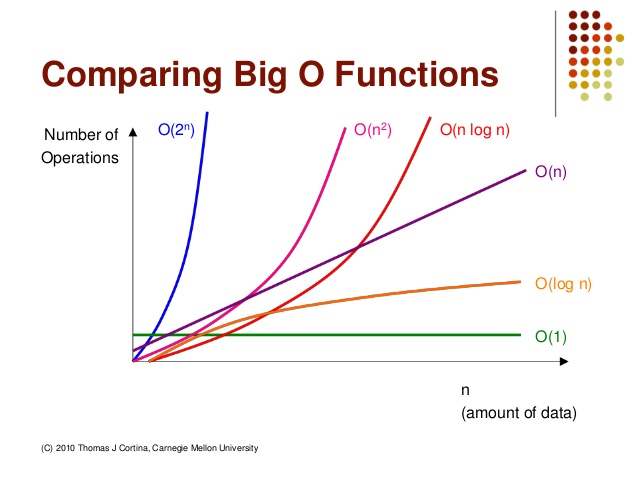
시간 복잡도
시간 복잡도란
알고리즘이 주어진 문제를 해결하기 위한 연산 횟수
시간 복잡도 유형
1.빅-오메가 Ω(n)
: 최선일 때(best case)의 연산 횟수를 나타내는 표기법
가장 빠른 케이스, 어떤 식의 최고 차수
2.빅-세타 𝚯(n)
: 보통일 때(average case)의 연산 횟수를 나타낸 표기법, 빅-오, 빅-오메가를 만족한느 교집합
평균 실행시간
3.빅-오 O(n)
: 최악일 때(worst case)의 연산 횟수를 나타낸 표기법
가장 느린 케이스
상수는 무시 혹은 1로 통일
상한선을 기준으로 하여 모든 경우의 수를 포함
빅-오 표기법을 기준으로 수행 시간을 계산하는 것이 좋은 이유
프로그램은 다양한 테스트 케이스를 수행하여 모든 케이스를 만족할만한 케이스를 염두해 둬야 하는데 그 경우가 최악의 시간까지 고려할 때이다.
[알고리즘] 시간복잡도(Time Complexity)와 Big-O표기법(Big-O Notation)
웹앱프로젝트를 진행하고 있지만 알고리즘관련 공부를 너무 등한시한 것 같아서 알고리즘 관련된 공부도 병행해서 진행해보려하고 관련내용을 블로그에 정리할 것입니다. 이에 앞서 알고리즘
velog.io
O(1) 상수 시간 - 입력 크기의 수와 상관없이 일정한 시간을 갖음
O(logN) 로그 시간 - logN의 경우 한 번 쪼갠 횟수만 계산하여 이진탐색 값을 찾을 때, NlogN의 경우 쪼갠 횟우의 모든 그룹을 계산하여 머지정렬일때 모든 부분을 탐색
O(N) 선형 시간 - 입력 값이 증가함에 따라 비례
O(N^2) 2차 시간 - 입력 값 n에 대해 이중for문, 삽입정렬, 버블정렬으로 n^2에 비례
O(2^N) 지수 시간 - 기하급수적 복잡도라 부르며 상수의 n제곱만큼 늘어나는 수행시간(피보나치, 재귀)
연산 횟수 계산 방법
연산 횟수 = 알고리즘 시간 복잡도 * 데이터의 크기
ex) 버블 정렬 = 100^2 = 10000 의 연산횟수가 필요
시간 복잡도 도출 기준
1.상수는 시간 복잡도 계산에서 제외
2.가장 많이 중첩된 반복문의 수행횟수가 시간 복잡도의 기준이 된다.
만약 일반 for문이 10개 더 있더라도 도출 원리의 기준에 따라 이중 for문의 시간 복잡도가 기준이 되어 n^2이 된다.
결과적으로 시간 복잡도를 고려하여 알고리즘을 설계하고 효율적으로 연산을 할 수 있으므로 실행 시간이 짧아진다.
정렬
기본 정렬 - 선택, 버블, 삽입
선택 정렬(Selection Sort)
선택 정렬(Selection Sort) - 현재 위치(인덱스)에 들어갈 데이터를 비교하면서 찾아 선택하여 나열하는 알고리즘
시간 복잡도 - O(n^2)

By Joestape89, CC BY-SA 3.0, 링크
File:Selection-Sort-Animation.gif - Wikimedia Commons
No higher resolution available.
commons.wikimedia.org
File:Selection sort animation.gif - Wikimedia Commons
No higher resolution available.
commons.wikimedia.org
Java 코드 - 선택 정렬
public static void main(String[] args) {
int[] array = {4, 2, 3, 11, 5, 20, 44, 8, 10, 7};
System.out.println(Arrays.toString(array));
System.out.println("start");
selectionSort(array);
System.out.println("end");
}
// 선택정렬
public static void selectionSort(int[] arr) {
int indexMin, temp;
// 배열 길이-1 만큼
for (int i = 0; i < arr.length - 1; i++) {
// 첫번째 인덱스 값을 최소 or 최대 인덱스값 지정
indexMin = i;
// 지정한 인덱스를 제외한 다음 인덱스부터
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[indexMin]) {
indexMin = j;
}
}
// 제일 작은 값의 인덱스를 가지고 있다가 반복문 종료시 swap
// swap
temp = arr[indexMin];
arr[indexMin] = arr[i];
arr[i] = temp;
System.out.println(Arrays.toString(arr));
}
}[4, 2, 3, 11, 5, 20, 44, 8, 10, 7]
start
[2, 4, 3, 11, 5, 20, 44, 8, 10, 7]
[2, 3, 4, 11, 5, 20, 44, 8, 10, 7]
[2, 3, 4, 11, 5, 20, 44, 8, 10, 7]
[2, 3, 4, 5, 11, 20, 44, 8, 10, 7]
[2, 3, 4, 5, 7, 20, 44, 8, 10, 11]
[2, 3, 4, 5, 7, 8, 44, 20, 10, 11]
[2, 3, 4, 5, 7, 8, 10, 20, 44, 11]
[2, 3, 4, 5, 7, 8, 10, 11, 44, 20]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
end
버블 정렬(Bubble Sort)
버블 정렬(Bubble Sort) - 정렬과정이 거품이 수면으로 올라오는 모습으로, 비교와 교환이 모두 일어나는 알고리즘
시간 복잡도 - O(n^2)
선택정렬과 결과는 동일하지만 과정이 다르고 속도가 더 느리다
File:Bubble sort animation.gif - Wikimedia Commons
File:Bubble sort animation.gif From Wikimedia Commons, the free media repository Jump to navigation Jump to search No higher resolution available.
commons.wikimedia.org
Java 코드 - 버블 정렬
public static void main(String[] args) {
int[] array = {4, 2, 3, 11, 5, 20, 44, 8, 10, 7};
System.out.println(Arrays.toString(array));
System.out.println("start");
bubbleSort(array);
System.out.println("end");
}
// 버블 정렬
public static void bubbleSort(int[] arr) {
int temp = 0;
for(int i = 0; i < arr.length - 1; i++) {
for(int j= 1 ; j < arr.length-i; j++) {
if(arr[j]<arr[j-1]) {
temp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = temp;
}
}
System.out.println(Arrays.toString(arr));
}
}[4, 2, 3, 11, 5, 20, 44, 8, 10, 7]
start
[2, 3, 4, 5, 11, 20, 8, 10, 7, 44]
[2, 3, 4, 5, 11, 8, 10, 7, 20, 44]
[2, 3, 4, 5, 8, 10, 7, 11, 20, 44]
[2, 3, 4, 5, 8, 7, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
end
삽입 정렬(Insertion Sort)
삽입 정렬(Insertion Sort) - 이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 알고리즘
시간 복잡도 - O(n^2)
File:Insertion sort animation.gif - Wikimedia Commons
No higher resolution available.
commons.wikimedia.org

File:Insertion sort.gif - Wikimedia Commons
No higher resolution available. Insertion_sort.gif (193 × 302 pixels, file size: 134 KB, MIME type: image/gif, looped, 255 frames, 28 s)
commons.wikimedia.org
Java 코드 - 삽입 정렬
public static void main(String[] args) {
int[] array = {4, 2, 3, 11, 5, 20, 44, 8, 10, 7};
System.out.println(Arrays.toString(array));
System.out.println("start");
insertionSort(array);
System.out.println("end");
}
// 삽입 정렬
public static void insertionSort(int[] arr)
{
for(int i = 1 ; i < arr.length ; i++){
int temp = arr[i];
int j = i - 1;
//더 작으면 계속 앞으로 전진시키면서 비교한 원소를 한 칸씩 뒤로 민다.
while( (j >= 0) && ( arr[j] > temp ) ) {
// swap
arr[j + 1] = arr[j];
j--; // 빈공간에 temp값을 넣기위해 감소
}
// swap
arr[j + 1] = temp;
System.out.println(Arrays.toString(arr));
}
}[4, 2, 3, 11, 5, 20, 44, 8, 10, 7]
start
[2, 4, 3, 11, 5, 20, 44, 8, 10, 7]
[2, 3, 4, 11, 5, 20, 44, 8, 10, 7]
[2, 3, 4, 11, 5, 20, 44, 8, 10, 7]
[2, 3, 4, 5, 11, 20, 44, 8, 10, 7]
[2, 3, 4, 5, 11, 20, 44, 8, 10, 7]
[2, 3, 4, 5, 11, 20, 44, 8, 10, 7]
[2, 3, 4, 5, 8, 11, 20, 44, 10, 7]
[2, 3, 4, 5, 8, 10, 11, 20, 44, 7]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
end
고급 정렬 - 병합, 퀵, 힙, 셸
합병,병합 정렬(Merge Sort)
합병,병합 정렬(Merge Sort) - 분할 정복 방식을 사용해 데이터를 분할하고 분할한 집합을 정렬하며 합치는 알고리즘이다.
분할(divide) - 정복(conquer) - 결합(combine) - 복사(copy), 분할, 정복, 결합을 재귀적으로 사용
시간 복잡도 - O(n log n)
원리
2개의 그룹으로 만들고 정렬한 후 투 포인터 개념을 사용하여 왼쪽, 오른쪽 그룹을 병합합니다.
병합하는 방법은 왼쪽 포인터와 오른쪽 포인터의 값을 비교하여 작은 값을 결과 배열에 추가하고 포인터를 오른쪽으로 1칸 이동시키는 원리이다.
File:Merge-sort-example-300px.gif - Wikimedia Commons
No higher resolution available.
commons.wikimedia.org
Java 코드 - 합병 정렬
public static void main(String[] args) {
int[] array = {4, 2, 3, 11, 5, 20, 44, 8, 10, 7};
System.out.println(Arrays.toString(array));
System.out.println("start");
sortByMergeSort(array);
System.out.println("end");
}
// 병합 정렬
public static void sortByMergeSort(int[] arr) {
// 배열과 동일한 길이의 임시 배열 생성
int[] tmpArr = new int[arr.length];
mergeSort(arr, tmpArr, 0, arr.length - 1);
System.out.println("result : "+Arrays.toString(arr));
}
public static void mergeSort(int[] arr, int[] tmpArr, int left, int right) {
if (left < right) {
// 2개의 그룹으로 나누기 위해 절반으로 나누다. 후에 재귀함수로 그 그룹의 절반을 나누어 정렬
int m = left + (right - left) / 2;
mergeSort(arr, tmpArr, left, m); // 좌측 그룹
mergeSort(arr, tmpArr, m + 1, right); // 우측 그룹
merge(arr, tmpArr, left, m, right); // 다시 병합
}
}
public static void merge(int[] arr, int[] tmpArr, int left, int mid, int right) {
// 정렬한 좌측 그룹부터 임시 배열로 이동 후 우측 그룹도 동일하게 동작
for (int i = left; i <= right; i++) {
tmpArr[i] = arr[i];
}
System.out.println(Arrays.toString(tmpArr));
int part1 = left;
int part2 = mid + 1;
int index = left;
while (part1 <= mid && part2 <= right) {
// 다시 재배열을 위해 임시배열에 병합된 두 그룹의 배열을 비교하여 더 작은 값을 추가하면 이동
if (tmpArr[part1] <= tmpArr[part2]) {
arr[index] = tmpArr[part1];
part1++;
} else {
arr[index] = tmpArr[part2];
part2++;
}
index++;
}
//while문이 끝나고 배열에 좌측 부분배열의 남은 것만 저장하는 이유는 다음과 같다.
//1. 우측 부분배열이 다 들어가고 좌측 부분배열만 남은 경우에는 좌측 부분 배열만 넣으면 됨.
//2. 좌측 부분배열이 다 들어가고 우측 부분배열만 남은 경우에는 이미 배열은 다 정렬된 것.
for (int i = 0; i <= mid - part1; i++) {
arr[index + i] = tmpArr[part1 + i];
}
}[4, 2, 3, 11, 5, 20, 44, 8, 10, 7]
start
[4, 2, 0, 0, 0, 0, 0, 0, 0, 0]
[2, 4, 3, 0, 0, 0, 0, 0, 0, 0]
[2, 4, 3, 11, 5, 0, 0, 0, 0, 0]
[2, 3, 4, 5, 11, 0, 0, 0, 0, 0]
[2, 3, 4, 5, 11, 20, 44, 0, 0, 0]
[2, 3, 4, 5, 11, 20, 44, 8, 0, 0]
[2, 3, 4, 5, 11, 20, 44, 8, 10, 7]
[2, 3, 4, 5, 11, 8, 20, 44, 7, 10]
[2, 3, 4, 5, 11, 7, 8, 10, 20, 44]
result : [2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
end
퀵 정렬(Quick Sort)
퀵 정렬(Quick Sort) - 기준점(피벗-pivot)을 사용해 해당 값보다 작은 데이터와 큰데이터로 분류하는 것을 반복해 정렬하는 알고리즘
합병 정렬과 같은 분할 정복 알고리즘으로 합병정렬은 일정한 부분으로 분할하지만 퀵정렬은 피벗 위치에 따라 다르게 분할한다.
시간 복잡도 - O(n log n)이나 최악의 경우 O(n^2)

By en:User:RolandH, CC BY-SA 3.0, 링크
File:Sorting quicksort anim.gif - Wikimedia Commons
No higher resolution available.
commons.wikimedia.org
Java 코드 - 퀵 정렬
public static void main(String[] args) {
int[] array = {4, 2, 3, 11, 5, 20, 44, 8, 10, 7};
System.out.println(Arrays.toString(array));
System.out.println("start");
sortByQuickSort(array);
System.out.println(Arrays.toString(array));
System.out.println("end");
}
// 퀵 정렬
public static void sortByQuickSort(int[] arr) {
quickSort(arr, 0, arr.length - 1);
}
public static void quickSort(int[] arr, int left, int right) {
// 분할
int part = partition(arr, left, right);
//반복하다 보면 자연스럽게 pivot 좌측에는 더 작은 값들이고 우측에는 더 큰 값들이다.
//끝나면 pivot의 위치인 left를 반환한다.
if (left < part - 1) {
quickSort(arr, left, part - 1);
}
if (part < right) {
quickSort(arr, part, right);
}
}
public static int partition(int[] arr, int left, int right) {
// 배열 합의 절반이나 특정위치(left,right)값에 따른 기준점
int pivot = arr[(left + right) / 2];
int tmp = 0;//swap
while (left <= right) {
//left의 원소 값이 pivot보다 클 때까지 증가 시키면서 찾는다.
//right의 원소 값이 pivot보다 작을 때까지 감소 시키면서 찾는다.
while (arr[left] < pivot) {
left++;
}
while (arr[right] > pivot) {
right--;
}
//둘다 찾았으면 두 원소를 교환한다.
if (left <= right) {
// swap
tmp = arr[left];
arr[left] = arr[right];
arr[right] = tmp;
left++;
right--;
}
}
return left;
}[4, 2, 3, 11, 5, 20, 44, 8, 10, 7]
start
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
end
힙 정렬(Heap Sort)
힙 정렬(Heap Sort) - 최대 힙, 최소힙을 구성해 정렬하는 방법
시간 복잡도 - O(n log n)

By RolandH, CC BY-SA 3.0, 링크
File:Sorting heapsort anim.gif - Wikimedia Commons
No higher resolution available.
commons.wikimedia.org
[ Heap ] 힙이란? 우선순위 큐란?
우선순위 큐는 배열, 연결리스트, 힙으로 구현가능하다 이 중에서 힙으로 구현하는 것이 가장 효율적이다 힙(Heap)이란 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다.
def-xyj.tistory.com
셸 정렬(Shell Sort)
셸 정렬(Shell Sort) - 삽입 정렬의 장점을 살리고 단점을 보완한 정렬 알고리즘
삽입될 위치에 따라 교환이 다수 발생한다는 단점
이를 보완하기 위해 일정 간격을 정하여 배열을 나누어 정렬하고 다시 간격을 줄여 정렬시키는 것을 반복한다.
시간 복잡도 - O(n^1.5)
File:Sorting shellsort anim.gif - Wikimedia Commons
No higher resolution available.
commons.wikimedia.org
Java 코드 - 셸 정렬
public static void main(String[] args) {
int[] array = {4, 2, 3, 11, 5, 20, 44, 8, 10, 7};
System.out.println(Arrays.toString(array));
System.out.println("start");
sortByShellSort(array);
System.out.println("end");
}
// 셸 정렬
public static void sortByShellSort(int[] arr) {
//h는일정 간격 값
// 삽입 정렬 후 간격을 반으로 줄이며 1이 될까지 반복
for (int h = arr.length / 2; h > 0; h /= 2) {
for (int i = h; i < arr.length; i++) {
int tmp = arr[i];
int j = i - h; //
while (j >= 0 && arr[j] > tmp) {
arr[j + h] = arr[j]; // 먼저 swap
j -= h; // 다시 빼주어
}
// 다시 빼준만큼 더해주므로 swap
arr[j + h] = tmp;
}
System.out.println("간격 : "+h+" : "+Arrays.toString(arr));
}
}[4, 2, 3, 11, 5, 20, 44, 8, 10, 7]
start
간격 : 5 : [4, 2, 3, 10, 5, 20, 44, 8, 11, 7]
간격 : 2 : [3, 2, 4, 7, 5, 8, 11, 10, 44, 20]
간격 : 1 : [2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
end
데이터 성질을 이용하는 정렬 알고리즘
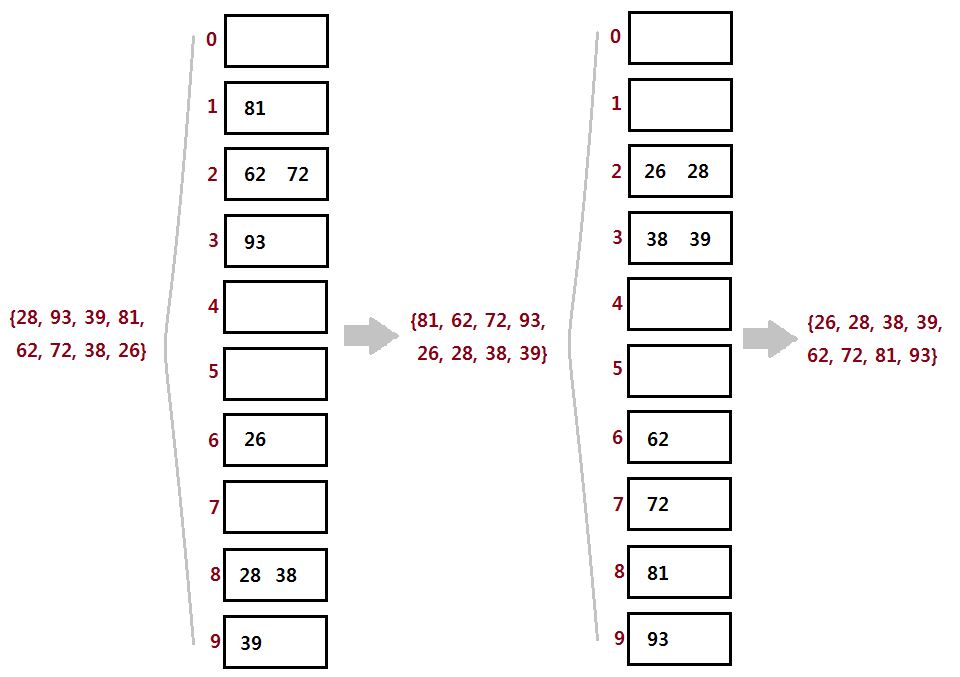
기수 정렬(Radix Sort)
기수 정렬(Radix Sort) - 값을 비교하지 않는 특이한 정렬으로 값을 놓고 비교할 자릿수를 정한 다음 해당 자릿수만 비교하는 알고리즘
시간 복잡도 - O(k n) k는 상수 k개이하의 자릿수
원리
큐를 이용해 자릿수의 데이터를 저장하고 정렬하는 과정을 반복하여 최종 정렬데이터를 도출하는 원리
일의 자릿수를 기준으로 데이터를 저장 -> 정렬 -> 십의 자릿수를 기준으로 저장 -> 정렬 -> …. -> 최종 정렬 데이터
https://sorjfkrh5078.tistory.com/21
기수 정렬(Radix Sort)
이번에 배워볼 정렬 알고리즘은 기수 정렬(Radix Sort)이다. 지금까지 배워온 정렬들은 모두 데이터들을 비교하여 정렬하는 방식이었다. 기수 정렬은 이와는 다르게 데이터를 비교하지 않고 정렬
sorjfkrh5078.tistory.com
Java 코드 - 기수 정렬
public static void main(String[] args) {
int[] array = {4, 2, 3, 11, 5, 20, 44, 8, 10, 7};
System.out.println(Arrays.toString(array));
System.out.println("start");
radix_Sort(array);
System.out.println("end");
}
// 기수 정렬
public static void radix_Sort(int[] arr) {
int n = arr.length;
//bucket 초기화
int bucketSize = 10;
Queue<Integer>[] bucket = new LinkedList[bucketSize];
for (int i = 0; i < bucketSize; ++i) {
bucket[i] = new LinkedList<>();
}
int factor = 1;
//정렬할 자릿수의 크기 만큼 반복한다.
for (int d = 0; d < 2; ++d) {
for (int i = 0; i < n; ++i) {
bucket[(arr[i] / factor) % 10].add(arr[i]);
}
System.out.println(factor+" : "+Arrays.toString(bucket));
// 재배열
for (int i = 0, j = 0; i < bucketSize; ++i) {
while (!bucket[i].isEmpty()) {
arr[j++] = bucket[i].poll();
}
System.out.println(Arrays.toString(arr));
}
// 자릿수 증가
factor *= 10;
}
}[4, 2, 3, 11, 5, 20, 44, 8, 10, 7]
start
1 : [[20, 10], [11], [2], [3], [4, 44], [5], [], [7], [8], []]
[20, 10, 3, 11, 5, 20, 44, 8, 10, 7]
[20, 10, 11, 11, 5, 20, 44, 8, 10, 7]
[20, 10, 11, 2, 5, 20, 44, 8, 10, 7]
[20, 10, 11, 2, 3, 20, 44, 8, 10, 7]
[20, 10, 11, 2, 3, 4, 44, 8, 10, 7]
[20, 10, 11, 2, 3, 4, 44, 5, 10, 7]
[20, 10, 11, 2, 3, 4, 44, 5, 10, 7]
[20, 10, 11, 2, 3, 4, 44, 5, 7, 7]
[20, 10, 11, 2, 3, 4, 44, 5, 7, 8]
[20, 10, 11, 2, 3, 4, 44, 5, 7, 8]
10 : [[2, 3, 4, 5, 7, 8], [10, 11], [20], [], [44], [], [], [], [], []]
[2, 3, 4, 5, 7, 8, 44, 5, 7, 8]
[2, 3, 4, 5, 7, 8, 10, 11, 7, 8]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 8]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 8]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
end
계수 정렬(Counting Sort)
계수 정렬(Counting Sort) - 숫자들간 비교를 하지 않고 정렬을 하는 알고리즘
각 숫자가 몇 개 있는지 개수를 세어 저장한 후에 정렬하는 방식
시간복잡도 - O(k n) 상수 k는 배열의 최대값
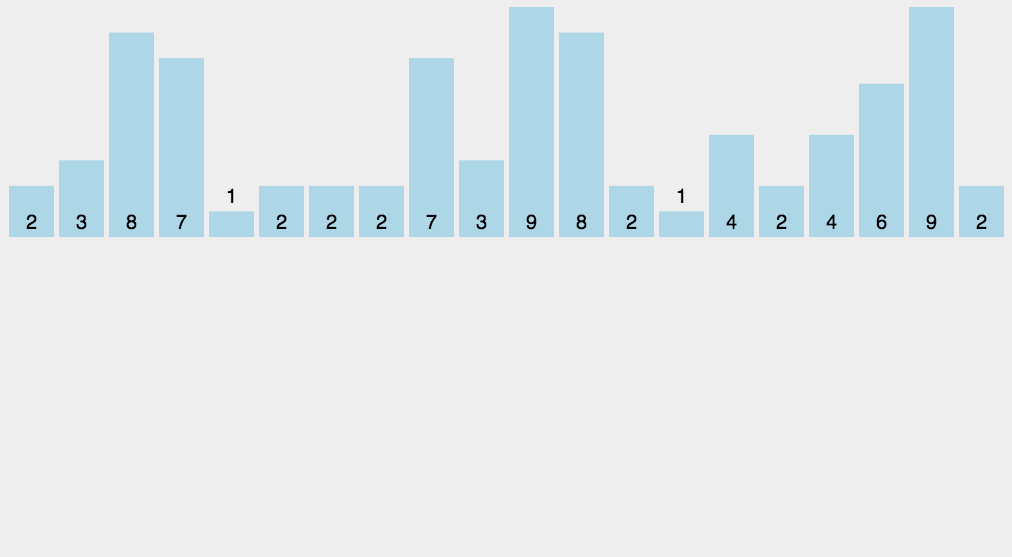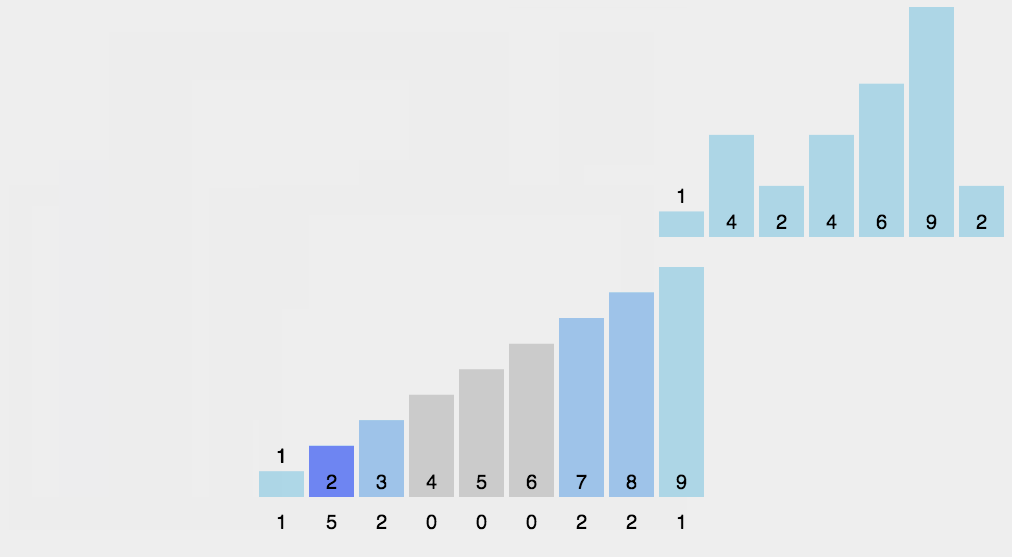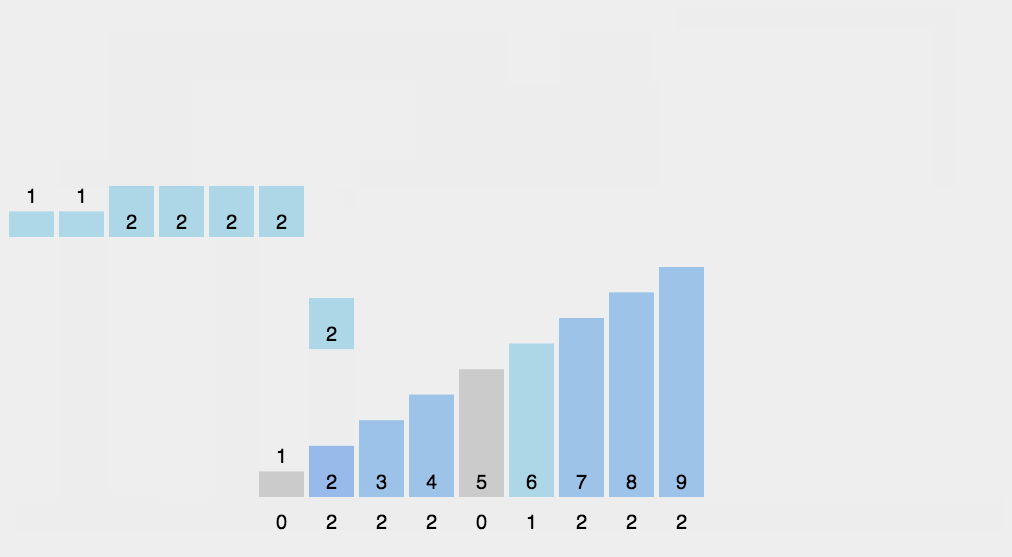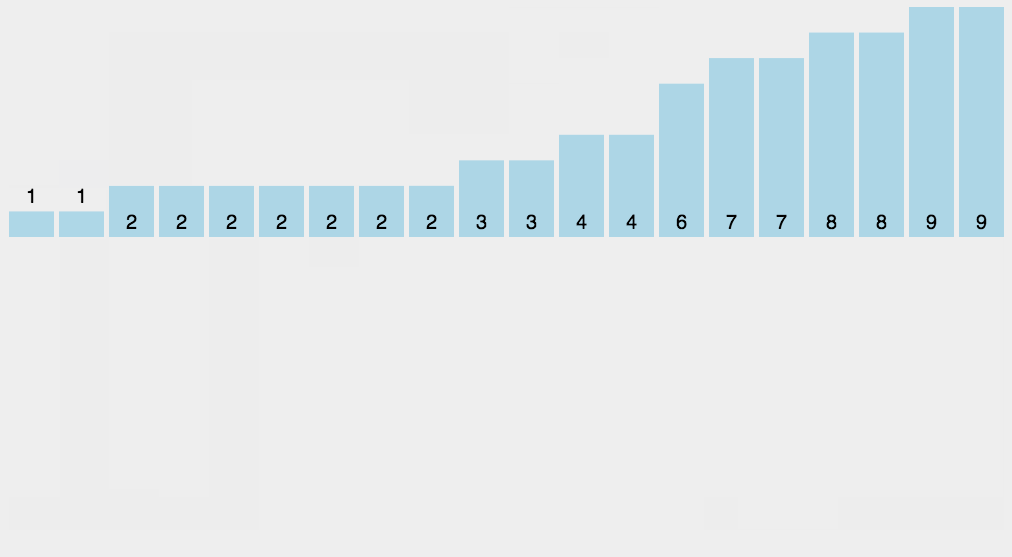
https://herong.tistory.com/entry/%EA%B3%84%EC%88%98%EC%A0%95%EB%A0%ACCounting-Sort
계수정렬(Counting Sort)
계수정렬(Counting Sort) 개념 Counting Sort는 숫자들간 비교를 하지 않고 정렬을 하는 알고리즘이다. 각 숫자가 몇개 있는지 개수를 세어 저장한 후에 정렬하는 방식이다. 로직 정렬하고자 하는 배열
herong.tistory.com
Java 코드 - 계수 정렬
public static void main(String[] args) {
int[] array = {4, 2, 3, 11, 5, 20, 44, 8, 10, 7};
System.out.println(Arrays.toString(array));
System.out.println("start");
countingSort(array);
System.out.println("end");
}
// 계수 정렬
public static void countingSort(int[] arr) {
int n = 10;
// 최대값 구하기
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
if (max < arr[i])
max = arr[i];
}
int[] counting = new int[max + 1]; // 카운팅 배열
for (int i = 0; i < 10; i++) {
counting[arr[i]]++;
}
System.out.println("최대 값 길이 : "+counting.length);
System.out.println(Arrays.toString(counting));
int index = 0;
for (int i = 0; i < counting.length; i++) {
while (counting[i]-- > 0) { // --, 0보다 큰 두가지 합친것
arr[index++] = i;
}
}
System.out.println(Arrays.toString(arr));
}[4, 2, 3, 11, 5, 20, 44, 8, 10, 7]
start
최대 값 길이 : 45
[0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
[2, 3, 4, 5, 7, 8, 10, 11, 20, 44]
end
정렬 참고
https://sorjfkrh5078.tistory.com/21
기수 정렬(Radix Sort)
이번에 배워볼 정렬 알고리즘은 기수 정렬(Radix Sort)이다. 지금까지 배워온 정렬들은 모두 데이터들을 비교하여 정렬하는 방식이었다. 기수 정렬은 이와는 다르게 데이터를 비교하지 않고 정렬
sorjfkrh5078.tistory.com
https://chb2005.tistory.com/75
[JAVA] 다양한 정렬 알고리즘 개념 및 시간 복잡도 비교
정렬 알고리즘 별 시간 복잡도 정렬 알고리즘 시간 복잡도 Bubble Sort (버블 정렬) O(n^2) Selection Sort (선택 정렬) O(n^2) Insertion Sort (삽입 정렬) O(n^2) Quick Sort (퀵 정렬) 평균 : O(nlogn) / 최악 : O(n^2) Merge S
chb2005.tistory.com
https://herong.tistory.com/entry/%EA%B3%84%EC%88%98%EC%A0%95%EB%A0%ACCounting-Sort
계수정렬(Counting Sort)
계수정렬(Counting Sort) 개념 Counting Sort는 숫자들간 비교를 하지 않고 정렬을 하는 알고리즘이다. 각 숫자가 몇개 있는지 개수를 세어 저장한 후에 정렬하는 방식이다. 로직 정렬하고자 하는 배열
herong.tistory.com
'코테 > 개념 정리' 카테고리의 다른 글
| DP - Dynamic Programming (동적 계획법) (0) | 2023.12.31 |
|---|---|
| 재귀, 이진탐색(Binary Search), 백트래킹(Backtracking) (1) | 2023.12.31 |
| 소수를 구하는 알고리즘 - 에라토스테네스의 체 (1) | 2023.12.27 |
| DFS( Depth first Search) - 깊이 우선 탐색 (1) | 2023.12.27 |
| BFS (Breadth First Search ) - 너비 우선 탐색 (0) | 2023.12.27 |






