DP - Dynamic Programming (동적 계획법)
복잡한 문제를 여러 개의 간단한 무제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법
원리
- 큰문제를 작은 문제로
- 작은 문제들이 반복돼 나타나고 사용되며 이 작은 문제들은 결괏값은 항상 같아야함
- 메모이제이션(Memoization)모든 작은 문제들은 한 번만 계산해 DP 테이블에 저장하며 추후 재상요할 때는 이 DP 테이블을 이용
- 톱다운 방식과 바텀 업 방식으로 구현
메모제이션 원리
피보나치 수열 구하는 공식은 f(n) = f(n-1) + f(n-2)으로 n번째 수열은 n-1번째 수열과 n-2번재 수열을 더한 값이다.
즉, 5번째 피보나치 수열은 4번째 와 3번째를 더한 값이고, 작은 문제로 나누면 4번째와 3번째로 나눌 수 있다. 이로 인해 피보나치 수열의 공식이 점화식으로 만들어지고 3번째 는 2번째와 1번째를 더한 값으로 이를 더한 값을 DP 테이블에 저장해 놓고 4번째 를 구할 때 재연산 할 필요 없이 DP 테이블에서 바로 값을 추출해서 사용하면 된다. 이러한 방식으로 사용하면 불필요한 연산과 탐색이 줄어들어 시간 복잡도 측면에서 많은 이점 이 있다.
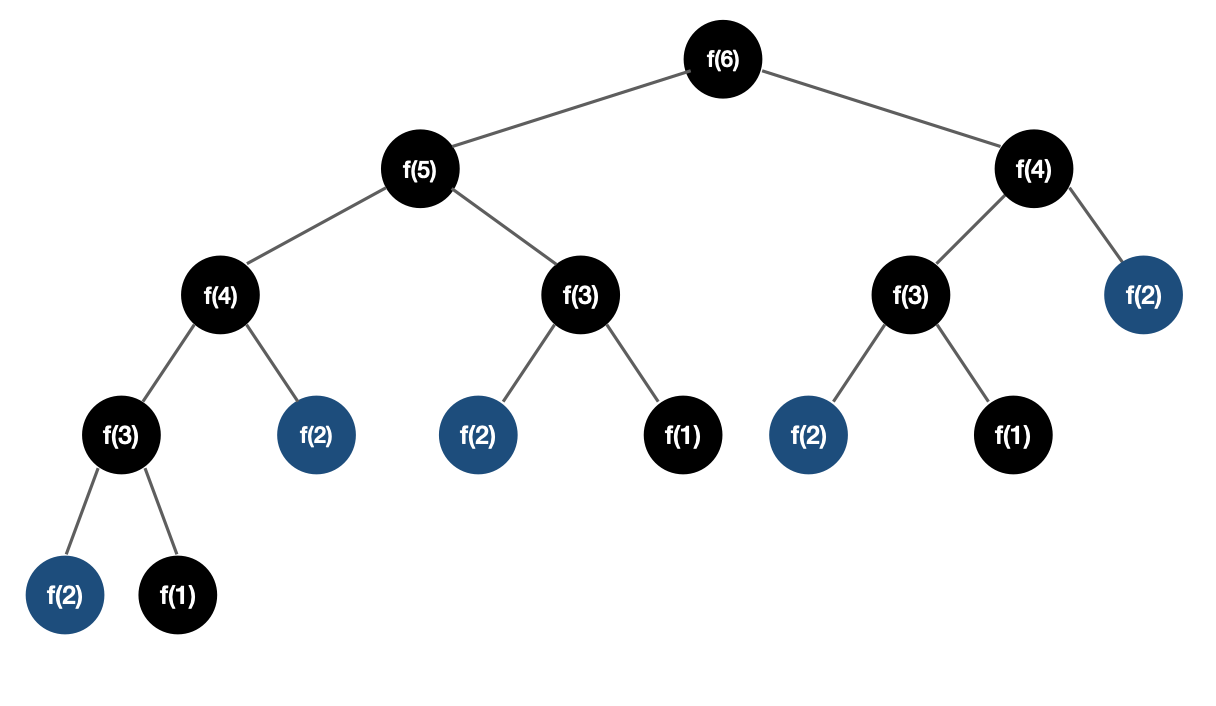
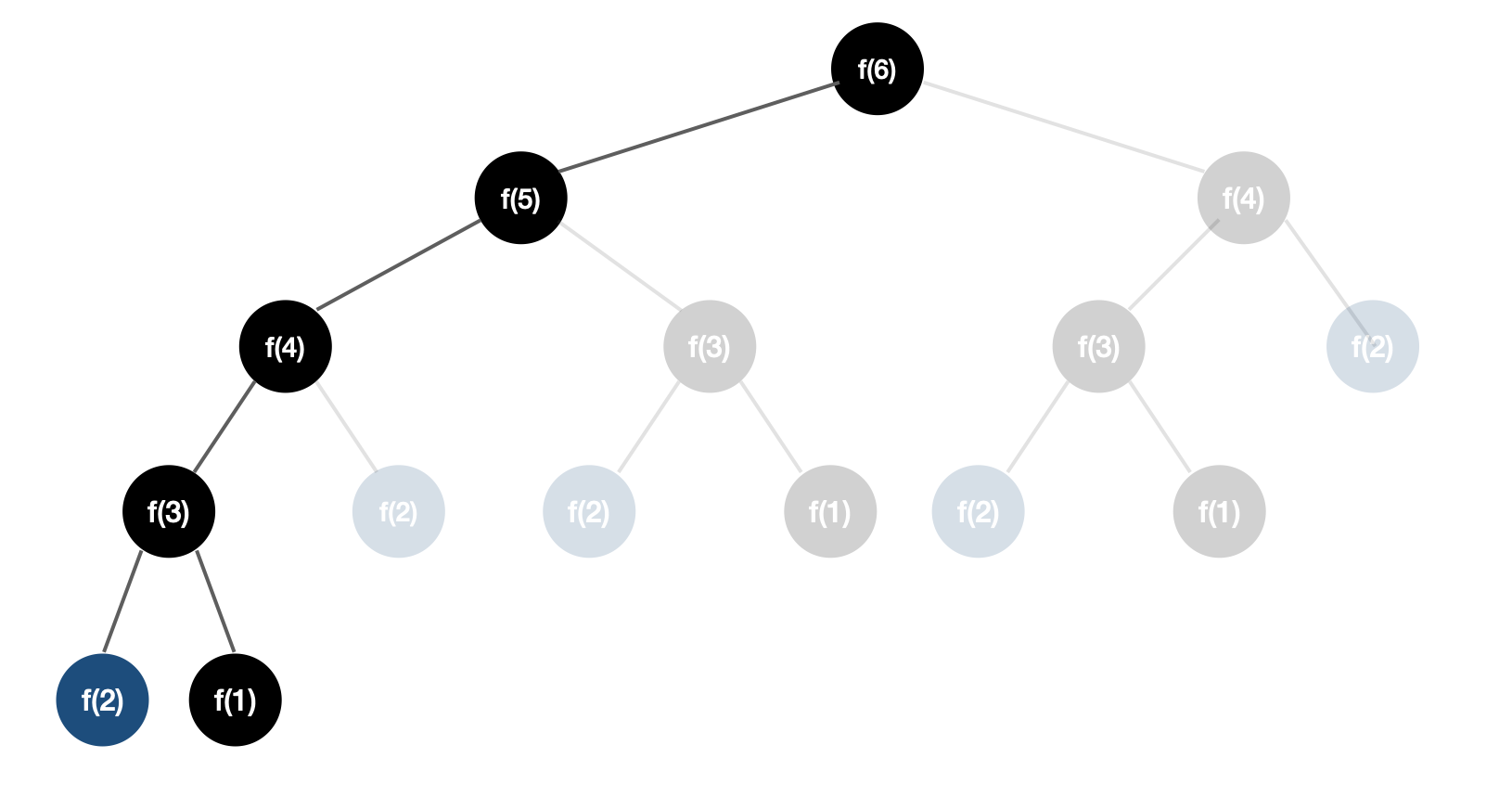
톱-다운(Top-Down) 방식 - 문제를 파악해 내려오는 방식으로, 주로 재귀함수 형태로 코드를 구현
static int[] f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int x = sc.nextInt();
f = new int[x+1];
for(int i=0; i<=x; i++) {
f[i] = -1;
}
f[0]=0;
f[1]=1;
fiboTopDown(x);
System.out.println(Arrays.toString(f));
}
public static int fiboTopDown(int n) {
System.out.println("n : "+n);
if(f[n] != -1)
return f[n];
return f[n] = fiboTopDown(n-1) + fiboTopDown(n-2); // 메모제이션
}5
n : 5
n : 4
n : 3
n : 2
n : 1
n : 0
n : 1
n : 2
n : 3
[0, 1, 1, 2, 3, 5]바텀-업(Bottom-up) 방식 - 가장 작은 부분 문제부터 문제를 해결하면서 점점 큰 문제로 확장해 나가는 방식으로, 주로 반복문 형태로 구현합니다.
static int[] f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int x = sc.nextInt();
f = new int[x+1];
for(int i=0; i<=x; i++) {
f[i] = -1;
}
f[0]=0;
f[1]=1;
fiboBottomUp(x);
System.out.println(Arrays.toString(f));
}
public static void fiboBottomUp(int n) {
for(int i=2; i<=n; i++) { // 작은 문제부터
f[i] = f[i-1] + f[i-2]; // 해결하면 메모제이션
System.out.println(Arrays.toString(f));
}
}5
[0, 1, 1, -1, -1, -1]
[0, 1, 1, 2, -1, -1]
[0, 1, 1, 2, 3, -1]
[0, 1, 1, 2, 3, 5]
[0, 1, 1, 2, 3, 5]
참고
'코테 > 개념 정리' 카테고리의 다른 글
| 슬라이딩 윈도우 알고리즘(백준 21921번) (1) | 2024.01.03 |
|---|---|
| 투 포인터 알고리즘(백준 2003번) (1) | 2024.01.03 |
| 재귀, 이진탐색(Binary Search), 백트래킹(Backtracking) (1) | 2023.12.31 |
| 시간복잡도, 정렬 알고리즘 (1) | 2023.12.31 |
| 소수를 구하는 알고리즘 - 에라토스테네스의 체 (1) | 2023.12.27 |
DP - Dynamic Programming (동적 계획법)
복잡한 문제를 여러 개의 간단한 무제로 분리하여 부분의 문제들을 해결함으로써 최종적으로 복잡한 문제의 답을 구하는 방법
원리
- 큰문제를 작은 문제로
- 작은 문제들이 반복돼 나타나고 사용되며 이 작은 문제들은 결괏값은 항상 같아야함
- 메모이제이션(Memoization)모든 작은 문제들은 한 번만 계산해 DP 테이블에 저장하며 추후 재상요할 때는 이 DP 테이블을 이용
- 톱다운 방식과 바텀 업 방식으로 구현
메모제이션 원리
피보나치 수열 구하는 공식은 f(n) = f(n-1) + f(n-2)으로 n번째 수열은 n-1번째 수열과 n-2번재 수열을 더한 값이다.
즉, 5번째 피보나치 수열은 4번째 와 3번째를 더한 값이고, 작은 문제로 나누면 4번째와 3번째로 나눌 수 있다. 이로 인해 피보나치 수열의 공식이 점화식으로 만들어지고 3번째 는 2번째와 1번째를 더한 값으로 이를 더한 값을 DP 테이블에 저장해 놓고 4번째 를 구할 때 재연산 할 필요 없이 DP 테이블에서 바로 값을 추출해서 사용하면 된다. 이러한 방식으로 사용하면 불필요한 연산과 탐색이 줄어들어 시간 복잡도 측면에서 많은 이점 이 있다.


톱-다운(Top-Down) 방식 - 문제를 파악해 내려오는 방식으로, 주로 재귀함수 형태로 코드를 구현
static int[] f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int x = sc.nextInt();
f = new int[x+1];
for(int i=0; i<=x; i++) {
f[i] = -1;
}
f[0]=0;
f[1]=1;
fiboTopDown(x);
System.out.println(Arrays.toString(f));
}
public static int fiboTopDown(int n) {
System.out.println("n : "+n);
if(f[n] != -1)
return f[n];
return f[n] = fiboTopDown(n-1) + fiboTopDown(n-2); // 메모제이션
}5
n : 5
n : 4
n : 3
n : 2
n : 1
n : 0
n : 1
n : 2
n : 3
[0, 1, 1, 2, 3, 5]바텀-업(Bottom-up) 방식 - 가장 작은 부분 문제부터 문제를 해결하면서 점점 큰 문제로 확장해 나가는 방식으로, 주로 반복문 형태로 구현합니다.
static int[] f;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int x = sc.nextInt();
f = new int[x+1];
for(int i=0; i<=x; i++) {
f[i] = -1;
}
f[0]=0;
f[1]=1;
fiboBottomUp(x);
System.out.println(Arrays.toString(f));
}
public static void fiboBottomUp(int n) {
for(int i=2; i<=n; i++) { // 작은 문제부터
f[i] = f[i-1] + f[i-2]; // 해결하면 메모제이션
System.out.println(Arrays.toString(f));
}
}5
[0, 1, 1, -1, -1, -1]
[0, 1, 1, 2, -1, -1]
[0, 1, 1, 2, 3, -1]
[0, 1, 1, 2, 3, 5]
[0, 1, 1, 2, 3, 5]
참고
'코테 > 개념 정리' 카테고리의 다른 글
| 슬라이딩 윈도우 알고리즘(백준 21921번) (1) | 2024.01.03 |
|---|---|
| 투 포인터 알고리즘(백준 2003번) (1) | 2024.01.03 |
| 재귀, 이진탐색(Binary Search), 백트래킹(Backtracking) (1) | 2023.12.31 |
| 시간복잡도, 정렬 알고리즘 (1) | 2023.12.31 |
| 소수를 구하는 알고리즘 - 에라토스테네스의 체 (1) | 2023.12.27 |
