우선순위 큐는
배열, 연결리스트, 힙으로 구현가능하다
이 중에서 힙으로 구현하는 것이 가장 효율적이다
힙(Heap)이란
완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다.
여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
힙은 일종의 반정렬 상태(느슨한 정렬)을 유지한다.
큰 값이 상위 레벨에 있고 작은 값이 하위레벨에 있다
간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 이진 트리를 말한다(부모 키 >= 자식 키)
힙 트리에서는 중복된 값을 허용한다.(하지만, 이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)
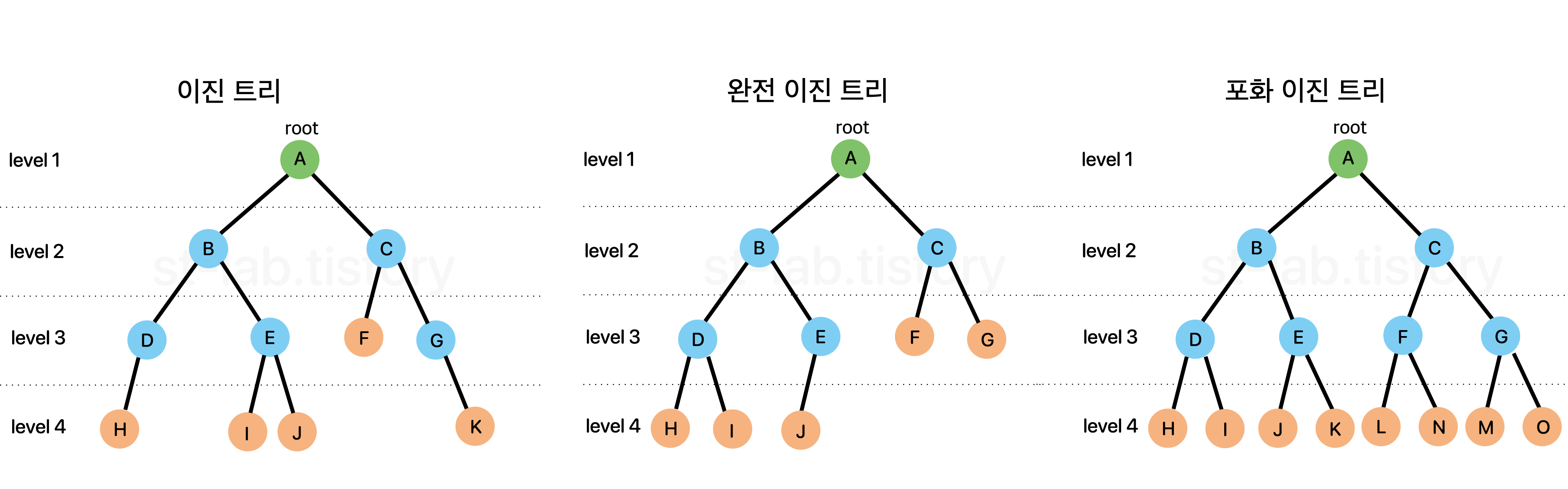
이진 트리
노드의 자식 노드를 최대 2개까지 갖는 트리
완전 이진 트리
마지막 레벨을 제외한 모든 노드가 채워져 있으면서 모든 노드(=마지막 레벨의 노드들)가 왼쪽부터 채워져 있어야 한다.
이 두 조건이 만족해야지 ‘완전 이진 트리’라고 한다.
포화 이진 트리
완전 이진 트리에서 한 가지 조건만 더 추가하면 포화 이진 트리라고 한다.
그건 바로 마지막 레벨을 제외한 모든 노드는 두 개의 자식 노드를 갖는다.
Heap 활용 예시
- 시뮬레이션 시스엠
- 네트워크 트래픽제어
- 운영 체제 작업 스케줄링
- 수치 계산
Heap의 종류
최대 힙(Max Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- 부모 노드 key >= 자식 노드 key
최소 힙(Min Heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
- 부모 노드 key <= 자식 노드 key

Heap 구현
힙을 저장하는 표준적인 자료구조는 배열 이다.
구현을 쉽게 하기 위하여 배열의 첫 번째 인덱스인 0은 사용하지 않는다.
특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
ex) 루트 노드의 오른쪽 노드의 번호는 항상 3이다.
힙에서의 부모 노드와 자식 노드의 관계
왼쪽 자식의 인덱스 는 부모의 인덱스에 2 곱한 값이다. Left Child Index = (Parent Index) * 2
오른쪽 자식의 인덱스는 부모의 인덱스에 2 곱한 값에 +1 이다. Right Child Index = (Parent Index) * 2 +1
부모의 인덱스는 자식의 인덱스를 2로 나눈 값이다. Parent Index = (Childe Index)/2

Heap 삽입(최대힙)
힙에 새로운 요소가 들어오면 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족 시킨다.
위의 과정을 위로 올라가면서 선별한다고 하여 Sift-Up 상향 선별 이라고 한다.

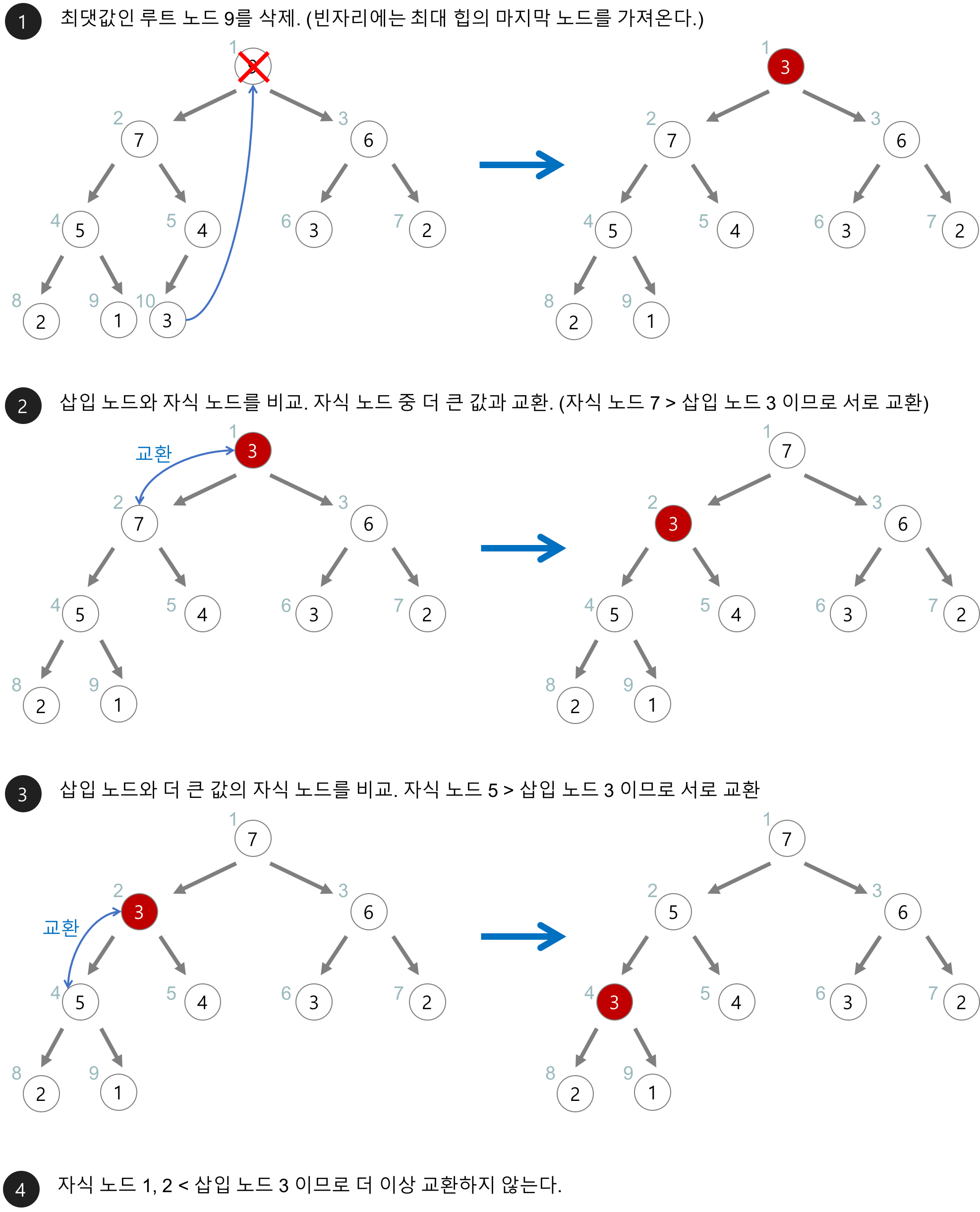
Heap 삭제(최대힙)
최대 힙에서 최댓값은 루트 노드이믈 루트 노드가 삭제된다.
최대 힙에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것이다.
삭제된 루트 노드에는 힙의 마지막 노드를 가져온다.
힙을 재구성한다.
최소힙의 경우 왼쪽 자식노드와 오른쪽 자식 노드 중 ‘작은 값을 가진 노드’랑 재배치가 들어간다.
이렇게 아래로 내려가면서 재배치 하는 과정을 Sift-Down 하향 선별이라고 한다.
코드
ArrayList로 구현한 최소 힙의 삽입 삭제
import java.util.ArrayList;
public class MinHeap {
private ArrayList<Integer> heap;
//최소힙 생성자
public MinHeap() {
heap = new ArrayList<Integer>();
heap.add(0); // 0번째 인덱스는 사용 안합
}
//삽입
public void insert(int x) {
heap.add(x);
// 1. 인덱스 생성
// p는 새로 삽입한 노드의 인덱스 정보
int p = heap.size()-1;
// 2. 최소힙에 조건에 맞게 스왑 반복
while(p>1 && heap.get(p/2)>heap.get(p)) {
//새로 삽입한 노드의 위치가 1 초과이고
//부모가 자식보다 크면 진행 ->새로 삽입한 노드의 위치가 루트까지 가거나 새로 삽입한 노드가 부모보다 클때까지 진행
//부모 노드의 값
int tmp = heap.get(p/2);
heap.set(p/2, x);
heap.set(p, tmp);
//새로 삽입한 노드가 한 레벨 상승했으니 인덱스 부모 노드 인덱스 값으로 변경
p /= 2;
}
}
//삭제
public int delete() {
//힙 이 비어있으면 0리턴
if(heap.size()-1 < 1) {
return 0;
}
//삭제할 노드, 루트 노드
int deleteitem = heap.get(1);
//마지막 노드를root에 삽입하고 마지막 노드 삭제
heap.set(1,heap.get(heap.size()-1));
heap.remove(heap.size()-1);
int pos = 1; //루트에 새로 삽입한 노드의 인덱스 정보
//pos*2는 왼쪽자식의 인덱스 값, 자식의 인덱스 값이 힙의 사이즈 값보다 크다는것은 더이상 삽입할 위치를 벗어났다는뜻
while((pos*2)<heap.size()) {
int min = heap.get(pos*2);//왼쪽 자식의 값
int minPos = pos*2;// 왼쪽 자식의 인덱스 값
//오른쪽 자식의 인덱스가 사이즈보다 작고 왼쪽 보다 더 작을때 오른쪽 자식을 부모와 바꿔줄 자식으로 지정
if(((pos*2+1)<heap.size()) && min > heap.get(pos*2+1)) {
min = heap.get(pos*2 +1);
minPos = pos*2 +1;
}
//부모가 더 작으면 그만
if(min > heap.get(pos))
break;
//부모 자식 교환
int tmp = heap.get(pos);
heap.set(pos,heap.get(minPos));
heap.set(minPos, tmp);
pos = minPos;
}
return deleteitem;
}
}
ArrayList로 구현한 최대힙의 삽입 삭제
import java.util.ArrayList;
public class MaxHeap {
private ArrayList<Integer> heap;
public MaxHeap() {
heap = new ArrayList<Integer>();
heap.add(0); //첫번째 인덱스는 사용하지 않음
}
//삽입
public void insert(int x) {
//맨 마지막 위치에 삽입
heap.add(x);
int p = heap.size()-1; //새로 넣은 노드의 인덱스 위치 정보
//루트까지 이동 자식이 더 크면 교환
while(p>1 && heap.get(p)> heap.get(p/2)) {
int tmp = heap.get(p/2);
heap.set(p/2, heap.get(p));
heap.set(p, tmp);
p /= 2;
}
}
//삭제
public int delete() {
//힙 이 비어있으면 0리턴
if(heap.size()-1 < 1) {
return 0;
}
//삭제할 루트 노드 값 저장
int deleteitem = heap.get(1);
//맨 마지막 자식 루트에 넣고 마지막 값 삭제
heap.set(1,heap.get(heap.size()-1));
heap.remove(heap.size()-1);
//루트에 새로 넣은 노드의 인덱스 정보
int pos = 1;
while((pos*2)<heap.size()) {
int max = heap.get(pos*2);
int maxPos = pos*2;
//오른쪽 자식이 존재하고 오른쪽 자식이 왼쪽 자식보다 클때 바꿀 자식 오른쪽으로 설정
if((pos*2 +1)<heap.size() && max < heap.get(pos*2+1)) {
max = heap.get(pos*2+1);
maxPos = pos*2+1;
}
//부모가 더 크면 끝
if(heap.get(pos) > max){
break;
}
//자식이 더 크면 교환
int tmp = heap.get(pos);
heap.set(pos, max);
heap.set(maxPos, tmp);
pos = maxPos;
}
return deleteitem;
}
}
참고
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
https://st-lab.tistory.com/205#%EC%A0%84%EC%B2%B4
https://ko.wikipedia.org/wiki/%ED%9E%99_(%EC%9E%90%EB%A3%8C_%EA%B5%AC%EC%A1%B0)
'코테 > 개념 정리' 카테고리의 다른 글
| Java 정렬과 Lamda 사용의 정렬 (0) | 2023.12.25 |
|---|---|
| java.uti.StringTokenizer 클래스 란? (0) | 2023.12.23 |
| 리스트 ArrayList <-> 배열 Array 변환 (1) | 2023.12.18 |
| 자료구조 - 스택(Stack) / 큐(Queue)에 관하여... (0) | 2023.12.09 |
| 자료구조 - 해시(Hash)에 관하여... (0) | 2023.12.09 |
